Многогранник получается при последовательном срезании каждой из вершин тетраэдра.
Усечённый тетраэдр является одним из 13 тел Архимеда.
Усечённый тетраэдр - полуправильный выпуклый многогранник, обладающий двумя свойствами:
1. Все грани являются правильными многоугольниками двух типов - шестиугольник и треугольник;
2. Для любой пары вершин существует симметрия многогранника (то
есть движение переводящее многогранник в себя) переводящая одну вершину в
другую.
Архимедовы тела являются полуправильными многогранниками в том
смысле, что их грани - правильные многоугольники, но они не одинаковы
при этом сохраняется условие одного из типов пространственной симметрии:
тетраэдрического, октаэдрического или икосаэдрического.
Этот многогранник будет выглядеть весьма эффектно,
если его шестиугольные грани раскрасить теми же цветами, в которые были
выкрашены четыре грани тетраэдра, а все треугольные грани сделать
одноцветными, используя новый цвет.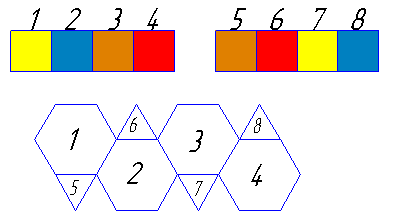 
Другой
способ раскраски основан на том, что каждая треугольная грань получает
тот же цвет, что и противоположная шестиугольная, параллельная ей.
Именно такую раскраску мы и приводим. Если вы подклеите все заготовки в указанном порядке, то получите развёртку с правильно раскрашенными гранями.
Вам остаётся только попарно склеить остальные наклейки способом, описанным для модели тетраэдра.
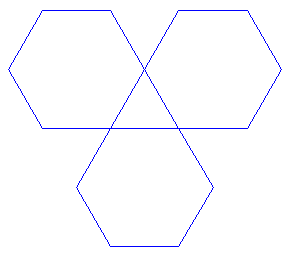Эту же модель можно построить и по-другому. Сначала вы делаете чашу в форме
тетраэдра, развёртка которой показана на рисунке слева. Дно чаши будет
треугольным, а стенки — шестиугольными. При этом соединённые наклейки
превратятся в жёсткие ребра по углам чаши, находящиеся внутри неё. Затем
вы склеиваете треугольники и шестиугольник между собой (лучше оставить
одну треугольную грань напоследок, крепко приклеив её только одной
стороной) и закрываете отверстие, как закрывают крышку ящика.
Такой способ рекомендуется применять при построении всех моделей.