 |
Древние греки дали многограннику имя по числу граней. «Окто»
означает восемь, «хедра» - означает грань (октаэдр – восьмигранник). Многогранник относится к правильным многогранникам и является одним из пяти платоновых тел.
Октаэдр имеет следующие характеристики:
-
Тип грани – правильный треугольник;
-
Число сторон у грани – 3;
-
Общее число граней – 8;
-
Число рёбер примыкающих к вершине – 4;
-
Общее число вершин – 6;
-
Общее число рёбер – 12;
Правильный октаэдр составлен из восьми равносторонних
треугольников. Каждая вершина октаэдра является вершиной четырех
треугольников. Следовательно, сумма плоских углов при каждой вершине
равна 240°.
Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии. |
Так как
его противоположные грани лежат в параллельных плоскостях, то можно
превосходно обойтись всего четырьмя красками.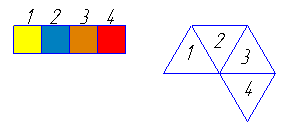 
Модель
этого многогранника вы начинаете делать, склеивая четыре треугольника,
как показано на рисунке справа. После того как вы склеите между собой
грани 1 и 4, в ваших руках окажется правильная четырёхугольная пирамида
без квадратного основания. Эта часть составляет ровно половину модели.
Вторая половина энантиоморфна первой. Тем не менее
проще продолжить работу в такой последовательности: сначала приклейте
наклейки четырёх оставшихся треугольников к соответствующим наклейкам на
сторонах квадратного основания. (Проследить, чтобы противоположные
грани октаэдра имели один и тот же цвет, нетрудно.) Затем
последовательно склейте наклейки соседних граней, снова закрывая модель
последним треугольником, как крышкой. Теперь вы можете заметить, что
квадрат, только что послуживший основанием первой половины модели, на
самом деле всего лишь один из трёх квадратов такого рода, которые можно
видеть на полной модели. При этом рёбра квадратов лежат в трёх взаимно
перпендикулярных плоскостях.