Древние греки дали многограннику имя по числу граней. «Тетра» означает четыре, «хедра» - означает грань (тетраэдр – четырехгранник). Многогранник относится к правильным многогранникам и является одним из пяти платоновых тел.
Тетраэдр имеет следующие характеристики:
- Тип грани – правильный треугольник;
- Число сторон у грани – 3;
- Общее число граней – 4;
- Число рёбер примыкающих к вершине – 3;
- Общее число вершин – 4;
- Общее число рёбер – 6;
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.
Простейшим среди многогранников является тетраэдр. Его четыре грани — равносторонние треугольники. Четыре — это наименьшее число граней, отделяющих часть трёхмерного пространства. Тем не менее тетраэдр обладает многими свойствами, характерными для однородных многогранников. Все его грани суть правильные многоугольники, причём каждая отделяется ребром в точности от одной грани. Все многогранные углы тетраэдра также равны между собой. Модель тетраэдра можно сделать, пользуясь одной развёрткой, на которой будут расположены все четыре треугольные грани. Однако в этом случае все грани будут одного цвета. Подобным же образом все выпуклые многогранники можно сделать с помощью одной развёртки и тем самым одноцветными. Если же вы хотите сделать модель тетраэдра (как и любого многогранника) разноцветной, следует приготовить развёртки для каждого типа грани в виде отдельного многоугольника. Для тетраэдра вам понадобится всего один трафарет в виде равностороннего треугольника.
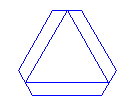
 Сделайте
четыре заготовки разного цвета. Не забудьте
оставить наклейки с каждой стороны, как показано на рисунке справа.
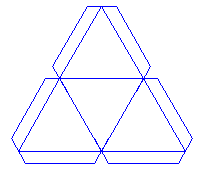
Теперь склейте все четыре заготовки вместе в положение, показанное
слева. Соедините несклеенные боковые грани и склейте вначале только две
из них между собой. Затем наложите клей на оставшиеся наклейки и
приклейте последнюю грань, как бы закрывая коробку. Дальнейшее сделают
внутренние напряжения в модели, ваши пальцы, приложенные к её ребрам, и
высыхающий клей.
Сделайте
четыре заготовки разного цвета. Не забудьте
оставить наклейки с каждой стороны, как показано на рисунке справа.
Теперь склейте все четыре заготовки вместе в положение, показанное
слева. Соедините несклеенные боковые грани и склейте вначале только две
из них между собой. Затем наложите клей на оставшиеся наклейки и
приклейте последнюю грань, как бы закрывая коробку. Дальнейшее сделают
внутренние напряжения в модели, ваши пальцы, приложенные к её ребрам, и
высыхающий клей.